Measurement Errors in R

Iñaki Ucar, Edzer Pebesma, Arturo Azcorra

Abstract

This paper presents an R package to handle and represent measurements with errors in a very simple way. We briefly introduce the main concepts of metrology and propagation of uncertainty, and discuss related R packages. Building upon this, we introduce the errors package, which provides a class for associating uncertainty metadata, automated propagation and reporting. Working with errors enables transparent, lightweight, less error-prone handling and convenient representation of measurements with errors. Finally, we discuss the advantages, limitations and future work of computing with errors.

$\newcommand{\E}{\mathbb{E}}$

This manuscript corresponds to errors version 0.4.2 and was typeset on 2024-07-29.
For citations, please use the version published in the R Journal (see citation("errors")).

Introduction

The International Vocabulary of Metrology (VIM) defines a quantity as “a property of a phenomenon, body, or substance, where the property has a magnitude that can be expressed as a number and a reference”, where most typically the number is a quantity value, attributed to a measurand and experimentally obtained via some measurement procedure, and the reference is a measurement unit (BIPM et al. 2012).

Additionally, any quantity value must accommodate some indication about the quality of the measurement, a quantifiable attribute known as uncertainty. The Guide to the Expression of Uncertainty in Measurement (GUM) defines uncertainty as “a parameter, associated with the result of a measurement, that characterises the dispersion of the values that could reasonably be attributed to the measurand” (BIPM et al. 2008). Uncertainty can be mainly classified into standard uncertainty, which is the result of a direct measurement (e.g., electrical voltage measured with a voltmeter, or current measured with a amperemeter), and combined standard uncertainty, which is the result of an indirect measurement (i.e., the standard uncertainty when the result is derived from a number of other quantities by the means of some mathematical relationship; e.g., electrical power as a product of voltage and current). Therefore, provided a set of quantities with known uncertainties, the process of obtaining the uncertainty of a derived measurement is called propagation of uncertainty.

Traditionally, computational systems have treated these three components (quantity values, measurement units and uncertainty) separately. Data consisted of bare numbers, and mathematical operations applied to them solely. Units were just metadata, and uncertainty propagation was an unpleasant task requiring additional effort and complex operations. Nowadays though, many software libraries have formalised quantity calculus as method of including units within the scope of mathematical operations, thus preserving dimensional correctness and protecting us from computing nonsensical combinations of quantities. However, these libraries rarely integrate uncertainty handling and propagation (Flater 2018).

Within the R environment, the units package (Pebesma and Mailund 2017; Pebesma, Mailund, and Hiebert 2016) defines a class for associating unit metadata to numeric vectors, which enables transparent quantity derivation, simplification and conversion. This approach is a very comfortable way of managing units with the added advantage of eliminating an entire class of potential programming mistakes. Unfortunately, neither units nor any other package address the integration of uncertainties into quantity calculus.

This article presents errors (Ucar 2018), a package that defines a framework for associating uncertainty metadata to R vectors, matrices and arrays, thus providing transparent, lightweight and automated propagation of uncertainty. This implementation also enables ongoing developments for integrating units and uncertainty handling into a complete solution.

Propagation of uncertainty

There are two main methods for propagation of uncertainty: the Taylor series method (TSM) and the Monte Carlo method (MCM). The TSM, also called the delta method, is based on a Taylor expansion of the mathematical expression that produces the output variables. As for the MCM, it can deal with generalised input distributions and propagates the uncertainty by Monte Carlo simulation.

Taylor series method

The TSM is a flexible and simple method of propagation of uncertainty that offers a good degree of approximation in most cases. In the following, we will provide a brief description. A full derivation, discussion and examples can be found in Arras (1998).

Mathematically, an indirect measurement is obtained as a function of $n$ direct or indirect measurements, $Y = f(X_1, ..., X_n)$, where the distribution of $X_n$ is unknown a priori. Usually, the sources of random variability are many, independent and probably unknown as well. Thus, the central limit theorem establishes that an addition of a sufficiently large number of random variables tends to a normal distribution. As a result, the first assumption states that $X_n$ are normally distributed.

The second assumption presumes linearity, i.e., that $f$ can be approximated by a first-order Taylor series expansion around $\mu_{X_n}$ (see Figure 1). Then, given a set of $n$ input variables $X$ and a set of $m$ output variables $Y$, the first-order uncertainty propagation law establishes that $$\begin{equation*} \Sigma_Y = J_X \Sigma_X J_X^T \tag{1} \end{equation*}$$ where $\Sigma$ is the covariance matrix and $J$ is the Jacobian operator.

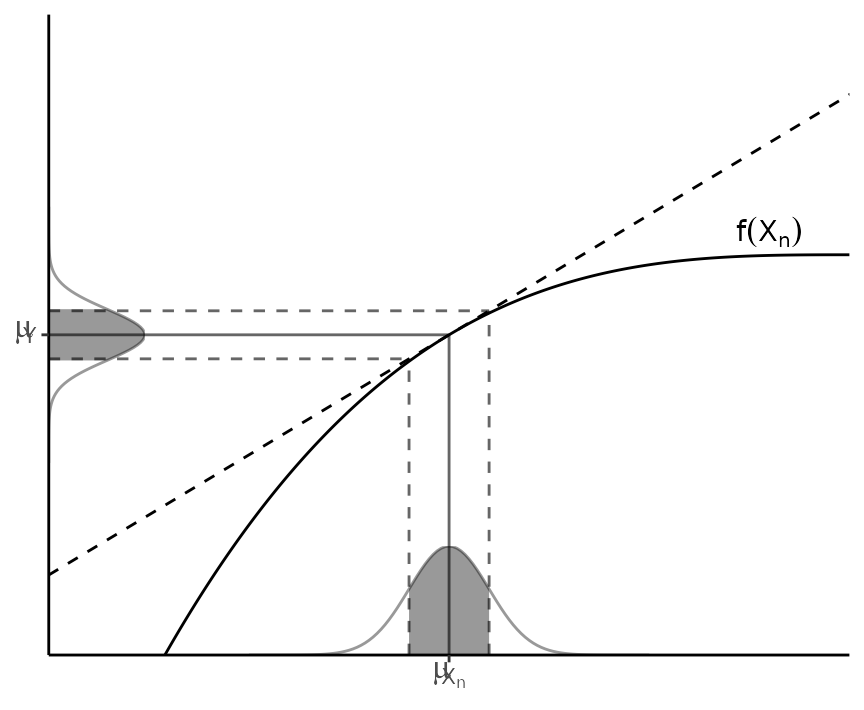
Figure 1: Illustration of linearity in an interval $\pm$ one standard deviation around the mean.

In practice, as recommended in the GUM (BIPM et al. 2008), this first-order approximation is good even if $f$ is non-linear, provided that the non-linearity is negligible compared to the magnitude of the uncertainty, i.e., $\E[f(X)]\approx f(\E[X])$. Also, this weaker condition is distribution-free: no assumptions are needed on the probability density functions (PDF) of $X_n$, although they must be reasonably symmetric.

If we consider Equation (1) for pairwise computations, i.e., $Y = f(X_1, X_2)$, we can write the propagation of the uncertainty $\sigma_Y$ as follows: $$\begin{equation*} \sigma_Y^2 = \left(\frac{\partial^2 f}{\partial X_1^2}\right)^2 \sigma_{X_1}^2 + \left(\frac{\partial^2 f}{\partial X_2^2}\right)^2 \sigma_{X_2}^2 + 2 \frac{\partial f \partial f}{\partial X_1 \partial X_2} \sigma_{X_1 X_2} \tag{2} \end{equation*}$$

The cross-covariances for the output $Y$ and any other variable $Z$ can be simplified as follows: $$\begin{equation*} \sigma_{Y Z} = \frac{\partial f}{\partial X_1} \sigma_{X_1 Z} + \frac{\partial f}{\partial X_2} \sigma_{X_2 Z} \tag{3} \end{equation*}$$ where, notably, if $Z=X_i$, one of the covariances above results in $\sigma_{X_i}^2$. Finally, and for the sake of completeness, the correlation coefficient can be obtained as $r_{Y Z} = \sigma_{Y Z} / (\sigma_{Y}\sigma_{Z})$.

Monte Carlo method

The MCM is based on the same principles underlying the TSM. It is based on the propagation of the PDFs of the input variables $X_n$ by performing random sampling and evaluating them under the model considered. Thus, this method is not constrained by the TSM assumptions, and explicitly determines a PDF for the output quantity $Y$, which makes it a more general approach that applies to a broader set of problems. For further details on this method, as well as a comparison with the TSM and some discussion on the applicability of both methods, the reader may refer to the Supplement 1 of the GUM (BIPM et al. 2008).

Reporting uncertainty

The GUM (BIPM et al. 2008) defines four ways of reporting standard uncertainty and combined standard uncertainty. For instance, if the reported quantity is assumed to be a mass $m_S$ of nominal value 100 g:

1. $m_S = 100.02147$ g with (a combined standard uncertainty) $u_c$ = 0.35 mg.
2. $m_S = 100.02147(35)$ g, where the number in parentheses is the numerical value of (the combined standard uncertainty) $u_c$ referred to the corresponding last digits of the quoted result.
3. $m_S = 100.02147(0.00035)$ g, where the number in parentheses is the numerical value of (the combined standard uncertainty) $u_c$ expressed in the unit of the quoted result.
4. $m_S = (100.02147 \pm 0.00035)$ g, where the number following the symbol $\pm$ is the numerical value of (the combined standard uncertainty) $u_c$ and not a confidence interval.

Schemes (2, 3) and (4) would be referred to as parenthesis notation and plus-minus notation respectively throughout this document. Although (4) is a very extended notation, the GUM explicitly discourages its use to prevent confusion with confidence intervals.

Related work

Several R packages are devoted to or provide methods for propagation of uncertainties. The car (Fox and Weisberg 2016, 2011) and msm (C. Jackson 2016; C. H. Jackson 2011) packages provide the functions deltaMethod() and deltamethod() respectively. Both of them implement a first-order TSM with a similar syntax, requiring a formula, a vector of values and a covariance matrix, thus being able to deal with dependency across variables.

The metRology (Ellison 2017) and propagate (Spiess 2014) packages stand out as very comprehensive sets of tools specifically focused on this topic, including both TSM and MCM. The metRology package implements TSM using algebraic or numeric differentiation, with support for correlation. It also provides a function for assessing the statistical performance of GUM uncertainty (TSM) using attained coverage probability. The propagate package implements TSM up to second order. It provides a unified interface for both TSM and MCM through the propagate() function, which requires an expression and a data frame or matrix as input. Unfortunately, as in the case of car and msm, these packages are limited to work only with expressions, which does not solve the issue of requiring a separate workflow to deal with uncertainties.

The spup package (Sawicka and Heuvelink 2017) focuses on uncertainty analysis in spatial environmental modelling, where the spatial cross-correlation between variables becomes important. The uncertainty is described with probability distributions and propagated using MCM.

Finally, the distr package (Kohl 2017; Ruckdeschel et al. 2006) takes this idea one step further by providing an S4-based object-oriented implementation of probability distributions, with which one can operate arithmetically or apply mathematical functions. It implements all kinds of probability distributions and has more methods for computing the distribution of derived quantities. Also, distr is the base of a whole family of packages, such as distrEllipse, distrEx, distrMod, distrRmetrics, distrSim and distrTeach.

All these packages provide excellent tools for uncertainty analysis and propagation. However, none of them addresses the issue of an integrated workflow, as units does for unit metadata by assigning units directly to R vectors, matrices and arrays. As a result, units can be added to any existing R computation in a very straightforward way. On the other hand, existing tools for uncertainty propagation require building specific expressions or data structures, and then some more work to extract the results out and to report them properly, with an appropriate number of significant digits.

Automated uncertainty handling in R: the errors package

The errors package aims to provide easy and lightweight handling of measurement with errors, including uncertainty propagation using the first-order TSM presented in the previous section and a formally sound representation.

Package description and usage

Standard uncertainties, can be assigned to numeric vectors, matrices and arrays, and then all the mathematical and arithmetic operations are transparently applied to both the values and the associated uncertainties:

library(errors)

x <- 1:5 + rnorm(5, sd = 0.01)
y <- 1:5 + rnorm(5, sd = 0.02)
errors(x) <- 0.01
errors(y) <- 0.02
x; y

## Errors: 0.01 0.01 0.01 0.01 0.01
## [1] 0.9859996 2.0025532 2.9756274 3.9999443 5.0062155

## Errors: 0.02 0.02 0.02 0.02 0.02
## [1] 1.022968 1.963564 2.995053 3.995116 4.994346

(z <- x / y)

## Errors: 0.021229025 0.011569056 0.007427156 0.005602416 0.004485713
## [1] 0.9638614 1.0198565 0.9935139 1.0012085 1.0023766

The errors() method assigns or retrieves a vector of uncertainties, which is stored as an attribute of the class errors, along with a unique object identifier:

str(x)

##  Errors: num [1:5] 0.99(1) 2.00(1) 2.98(1) 4.00(1) 5.01(1)

Correlations (and thus covariances) between pairs of variables can be set and retrieved using the correl() and covar() methods. These correlations are stored in an internal hash table indexed by the unique object identifier assigned to each errors object. If an object is removed, its associated correlations are cleaned up automatically.

correl(x, x) # one, cannot be changed

## [1] 1 1 1 1 1

correl(x, y) # NULL, not defined yet

## NULL

correl(x, y) <- runif(length(x), -1, 1)
correl(x, y)

## [1] -0.4202154  0.3567609  0.4706392 -0.6080865  0.9610793

covar(x, y)

## [1] -8.404308e-05  7.135217e-05  9.412784e-05 -1.216173e-04  1.922159e-04

Internally, errors provides S3 methods for the generics belonging to the groups Math and Ops, which propagate the uncertainty and the covariance using Equations (2) and (3) respectively.

z # previous computation without correlations

## Errors: 0.021229025 0.011569056 0.007427156 0.005602416 0.004485713
## [1] 0.9638614 1.0198565 0.9935139 1.0012085 1.0023766

(z_correl <- x / y)

## Errors: 0.024606702 0.009802843 0.005857672 0.006829703 0.002161687
## [1] 0.9638614 1.0198565 0.9935139 1.0012085 1.0023766

Other many S3 methods are also provided, such as generics belonging to the Summary group, subsetting operators ([, [<-, [[, [[<-), concatenation (c()), differentiation (diff), row and column binding (rbind, cbind), coercion to list, data frame and matrix, and more. Such methods mutate the errors object, and thus return a new one with no correlations associated. There are also setters defined as an alternative to the assignment methods (set_*() instead of errors<-, correl<- and covar<-), primarily intended for their use in conjunction with the pipe operator (%>%) from the magrittr (Bache and Wickham 2014) package.

Additionally, other useful summaries are provided, namely, the mean, the weighted mean and the median. The uncertainty of any measurement of central tendency cannot be smaller than the uncertainty of the individual measurements. Therefore, the uncertainty assigned to the mean is computed as the maximum between the standard deviation of the mean and the mean of the individual uncertainties (weighted, in the case of the weighted mean). As for the median, its uncertainty is computed as $\sqrt{\pi/2}\approx1.253$ times the standard deviation of the mean, where this constant comes from the asymptotic variance formula (Hampel et al. 2011).

It is worth noting that both values and uncertainties are stored with all the digits. However, when a single measurement or a column of measurements in a data frame are printed, there are S3 methods for format() and print() defined to properly format the output and display a single significant digit for the uncertainty. This default representation can be overridden using the digits option, and it is globally controlled with the option errors.digits.

# the elementary charge
e <- set_errors(1.6021766208e-19, 0.0000000098e-19)
print(e, digits = 2)

## 1.6021766208(98)e-19

The parenthesis notation, in which the number in parentheses is the uncertainty referred to the corresponding last digits of the quantity value (scheme 2 from the GUM, widely used in physics due to its compactness), is used by default, but this can be overridden through the appropriate option in order to use the plus-minus notation instead.

options(errors.notation = "plus-minus")
print(e, digits = 2)

## (1.6021766208 ± 0.0000000098)e-19

options(errors.notation = "parenthesis")

Finally, errors also facilitates plotting of error bars. In the following, we first assign a 2% of uncertainty to all the numeric variables in the iris data set and then we plot it using base graphics and ggplot2 (Wickham and Chang 2016; Wickham 2009). The result is shown in Figure 2.

iris.e <- iris
iris.e[1:4] <- lapply(iris.e[1:4], function(x) set_errors(x, x*0.02))

head(iris.e)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1       5.1(1)     3.50(7)      1.40(3)    0.200(4)  setosa
## 2       4.9(1)     3.00(6)      1.40(3)    0.200(4)  setosa
## 3      4.70(9)     3.20(6)      1.30(3)    0.200(4)  setosa
## 4      4.60(9)     3.10(6)      1.50(3)    0.200(4)  setosa
## 5       5.0(1)     3.60(7)      1.40(3)    0.200(4)  setosa
## 6       5.4(1)     3.90(8)      1.70(3)    0.400(8)  setosa

plot(Sepal.Width ~ Sepal.Length, iris.e, col=Species)
legend(6.2, 4.4, unique(iris.e[["Species"]]),
       col=1:length(iris.e[["Species"]]), pch=1)

library(ggplot2)

ggplot(iris.e) + aes(Sepal.Length, Sepal.Width, color=Species) +
  geom_point() + geom_errors() + theme_bw() + theme(legend.position=c(0.6, 0.8))

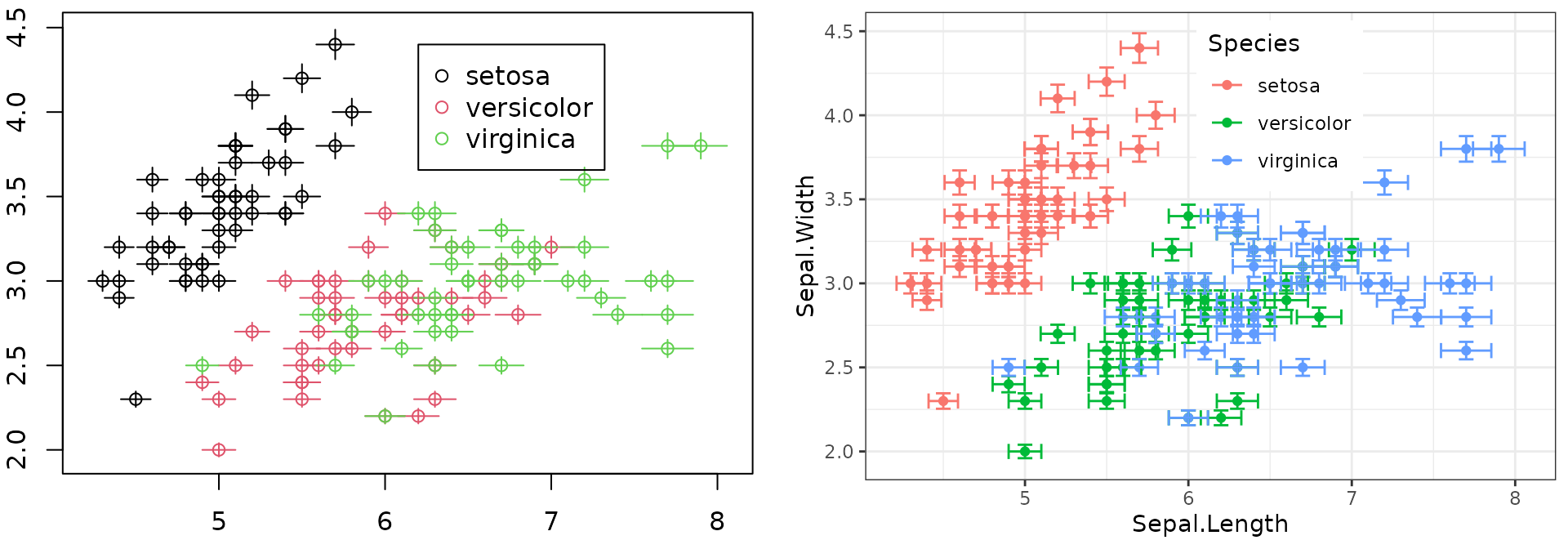
Figure 2: Base plot with error bars (left) and ggplot2’s version (right).

In base graphics, the error bars are automatically plotted when an object of class errors is passed. Additionally, we provide the convenience functions errors_min(x) and errors_max(x) for obtaining the boundaries of the interval in ggplot2 and other plotting packages, instead of writing x - errors(x) and x + errors(x) respectively.

Example: Simultaneous resistance and reactance measurement

From Annex H.2 of the GUM (BIPM et al. 2008):

The resistance $R$ and the reactance $X$ of a circuit element are determined by measuring the amplitude $V$ of a sinusoidally-alternating potential difference across its terminals, the amplitude $I$ of the alternating current passing through it, and the phase-shift angle $\phi$ of the alternating potential difference relative to the alternating current.

The measurands (resistance $R$, reactance $X$ and impedance $Z$) are related to the input quantities ($V$, $I$, $phi$) by the Ohm’s law: $$\begin{equation*} R = \frac{V}{I}\cos\phi; \qquad X = \frac{V}{I}\sin\phi; \qquad Z = \frac{V}{I} \tag{4} \end{equation*}$$

Five simultaneous observations for each input variable are provided (Table H.2 of the GUM), which are included in errors as dataset GUM.H.2. First, we need to obtain the mean input values and set the correlations from the measurements. Then, we compute the measurands and examine the correlations between them. The results agree with those reported in the GUM:

V   <- mean(set_errors(GUM.H.2$V))
I   <- mean(set_errors(GUM.H.2$I))
phi <- mean(set_errors(GUM.H.2$phi))

correl(V, I)   <- with(GUM.H.2, cor(V, I))
correl(V, phi) <- with(GUM.H.2, cor(V, phi))
correl(I, phi) <- with(GUM.H.2, cor(I, phi))

print(R <- (V / I) * cos(phi), digits = 2, notation = "plus-minus")

## 127.732 ± 0.071

print(X <- (V / I) * sin(phi), digits = 3, notation = "plus-minus")

## 219.847 ± 0.296

print(Z <- (V / I), digits = 3, notation = "plus-minus")

## 254.260 ± 0.236

correl(R, X); correl(R, Z); correl(X, Z)

## [1] -0.5884298

## [1] -0.4852592

## [1] 0.9925116

Example: Calibration of a thermometer

From Annex H.3 of the GUM (BIPM et al. 2008):

A thermometer is calibrated by comparing $n=11$ temperature readings $t_k$ of the thermometer […] with corresponding known reference temperatures $t_{R,k}$ in the temperature range 21 $^\circ$C to 27 $^\circ$C to obtain the corrections $b_k=t_{R,k}-t_k$ to the readings.

Measured temperatures and corrections (Table H.6 of the GUM), which are included in errors as dataset GUM.H.3, are related by a linear calibration curve: $$\begin{equation*} b(t) = y_1 + y_2 (t - t_0) \tag{5} \end{equation*}$$

In the following, we first fit the linear model for a reference temperature $t_0=20$$^\circ$C. Then, we extract the coefficients, and assign the uncertainty and correlation between them. Finally, we compute the predicted correction $b(30)$, which agrees with the value reported in the GUM:

fit <- lm(bk ~ I(tk - 20), data = GUM.H.3)

y1 <- set_errors(coef(fit)[1], sqrt(vcov(fit)[1, 1]))
y2 <- set_errors(coef(fit)[2], sqrt(vcov(fit)[2, 2]))
covar(y1, y2) <- vcov(fit)[1, 2]

print(b.30 <- y1 + y2 * set_errors(30 - 20), digits = 2, notation = "plus-minus")

## -0.1494 ± 0.0041

Discussion

The errors package provides the means for defining numeric vectors, matrices and arrays with errors in R, as well as to operate with them in a transparent way. Propagation of uncertainty implements the commonly used first-order TSM formula from Equation (1). This method has been pre-computed and expanded for each operation in the S3 groups Math and Ops, instead of differentiating symbolic expressions on demand or using functions from other packages for this task. The advantages of this approach are twofold. On the one hand, it is faster, as it does not involve simulation nor symbolic computation, and very lightweight in terms of package dependencies.

Another advantage of errors is the built-in consistent and formally sound representation of measurements with errors, rounding the uncertainty to one significant digit by default and supporting two widely used notations: parenthesis (e.g., $5.00(1)$) and plus-minus (e.g., $5.00 \pm 0.01$). These notations are applied for single numbers and data frames, as well as tbl_df data frames from the tibble (Wickham, Francois, and Müller 2017) package.

Full support is provided for both data.frame and tbl_df, as well as matrices and arrays. However, some operations on those data structures may drop uncertainties (i.e., object class and attributes). More specifically, there are six common data wrangling operations: row subsetting, row ordering, column transformation, row aggregation, column joining and (un)pivoting. Table 1 shows the correspondence between these operations and R base functions, as well as the compatibility with errors.

Table 1: Compatibility of errors and R base data wrangling functions.

Operation	R base function(s)	Compatibility
Row subsetting	[, [[, subset	Full
Row ordering	order + [	Full
Column transformation	transform, within	Full
Row aggregation	tapply, by, aggregate	with simplify=FALSE
Column joining	merge	Full
(Un)Pivoting	reshape	Full

Overall, errors is fully compatible with data wrangling operations embed in R base, and this is because those functions are mainly based on the subsetting generics, for which errors provides the corresponding S3 methods. Nonetheless, special attention must be paid to aggregations, which store partial results in lists that are finally simplified. Such simplification is made with unlist, which drops all the input attributes, including custom classes. However, all these aggregation functions provide the argument simplify (sometimes SIMPLIFY), which if set to FALSE, prevents this destructive simplification, and lists are returned. Such lists can be simplified non-destructively by calling do.call(c, ...).

unlist <- function(x) if (is.list(x)) do.call(c, x) else x
iris.e.agg <- aggregate(. ~ Species, data = iris.e, mean, simplify=FALSE)
as.data.frame(lapply(iris.e.agg, unlist), col.names=colnames(iris.e.agg))

##      Species Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1     setosa       5.0(1)     3.43(7)      1.46(3)     0.25(1)
## 2 versicolor       5.9(1)     2.77(6)      4.26(9)     1.33(3)
## 3  virginica       6.6(1)     2.97(6)       5.6(1)     2.03(4)

Summary and future work

We have introduced errors, a lightweight R package for managing numeric data with associated standard uncertainties. The new class errors provides numeric operations with automated propagation of uncertainty through a first-order TSM, and a formally sound representation of measurements with errors. Using this package makes the process of computing indirect measurements easier and less error-prone.

Future work includes importing and exporting data with uncertainties and providing the user with an interface for plugging uncertainty propagation methods from other packages. Finally, errors enables ongoing developments for integrating units and uncertainty handling into a complete solution for quantity calculus. Having a unified workflow for managing measurements with units and errors would be an interesting addition to the R ecosystem with very few precedents in other programming languages.

References

Arras, K. O. 1998. “An Introduction to Error Propagation: Derivation, Meaning and Examples of Cy = Fx Cx Fx’,” September.

Bache, Stefan Milton, and Hadley Wickham. 2014. Magrittr: A Forward-Pipe Operator for r. https://CRAN.R-project.org/package=magrittr.

BIPM, IEC, IFCC, ILAC, IUPAC, IUPAP, ISO, and OIML. 2008. “Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement, 1st edn. JCGM 100:2008.” Joint Committee for Guides in Metrology. https://www.bipm.org/en/committees/jc/jcgm/publications.

———. 2012. “The International Vocabulary of Metrology – Basic and General Concepts and Associated Terms (VIM), 3rd edn. JCGM 200:2012.” Joint Committee for Guides in Metrology. https://www.bipm.org/en/committees/jc/jcgm/publications.

Ellison, Stephen L R. 2017. metRology: Support for Metrological Applications. https://CRAN.R-project.org/package=metRology.

Flater, David. 2018. “Architecture for software-assisted quantity calculus.” Computer Standards & Interfaces 56: 144–47. https://doi.org/10.1016/j.csi.2017.10.002.

Fox, John, and Sanford Weisberg. 2011. An R Companion to Applied Regression. Second. SAGE Publications.

———. 2016. Car: Companion to Applied Regression. https://CRAN.R-project.org/package=car.

Hampel, F. R., E. M. Ronchetti, P. J. Rousseeuw, and W. A. Stahel. 2011. Robust Statistics: The Approach Based on Influence Functions. Wiley Series in Probability and Statistics. Wiley.

Jackson, Christopher. 2016. Msm: Multi-State Markov and Hidden Markov Models in Continuous Time. https://CRAN.R-project.org/package=msm.

Jackson, Christopher H. 2011. “Multi-State Models for Panel Data: The msm Package for R.” Journal of Statistical Software 38 (8): 1–29. https://doi.org/10.18637/jss.v038.i08.

Kohl, Matthias. 2017. Distr: Object Oriented Implementation of Distributions. https://CRAN.R-project.org/package=distr.

Pebesma, Edzer, and Thomas Mailund. 2017. Units: Measurement Units for r Vectors. https://CRAN.R-project.org/package=units.

Pebesma, Edzer, Thomas Mailund, and James Hiebert. 2016. “Measurement Units in R.” The R Journal 8 (2): 486–94. https://journal.r-project.org/archive/2016/RJ-2016-061/index.html.

Ruckdeschel, P., M. Kohl, T. Stabla, and F. Camphausen. 2006. “S4 Classes for Distributions.” R News 6 (2): 2–6.

Sawicka, Kasia, and Gerard Heuvelink. 2017. Spup: Uncertainty Propagation Analysis. https://CRAN.R-project.org/package=spup.

Spiess, Andrej-Nikolai. 2014. Propagate: Propagation of Uncertainty. https://CRAN.R-project.org/package=propagate.

Ucar, Iñaki. 2018. Errors: Uncertainty Propagation for r Vectors. https://CRAN.R-project.org/package=errors.

Wickham, Hadley. 2009. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York.

Wickham, Hadley, and Winston Chang. 2016. Ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. https://CRAN.R-project.org/package=ggplot2.

Wickham, Hadley, Romain Francois, and Kirill Müller. 2017. Tibble: Simple Data Frames. https://CRAN.R-project.org/package=tibble.