Units of Measurement for R Vectors: an Introduction

R has little support for physical measurement units. The exception is formed by time differences: time differences objects of class difftime have a units attribute that can be modified:

t1 = Sys.time() 
t2 = t1 + 3600 
d = t2 - t1
class(d)
## [1] "difftime"
units(d)
## [1] "hours"
d
## Time difference of 1 hours
units(d) = "secs"
d
## Time difference of 3600 secs

We see here that the units method is used to retrieve and modify the unit of time differences.

The units package generalizes this idea to other physical units, building upon the udunits2 C library. The udunits2 library provides the following operations:

validating whether an expression, such as m/s is a valid physical unit
verifying whether two units such as m/s and km/h are convertible
converting values between two convertible units
providing names and symbols for specific units
handle different character encodings (utf8, ascii, iso-8859-1 and latin1)

The units R package uses the udunits2 C library to extend R with functionality for manipulating numeric vectors that have physical measurement units associated with them, in a similar way as difftime objects behave.

Setting units, unit conversion

We can set units to numerical values by set_units:

library(units)
## udunits database from /usr/share/xml/udunits/udunits2.xml
(a <- set_units(runif(10),  m/s))
## Units: [m/s]
##  [1] 0.85175947 0.09059982 0.25062882 0.75417699 0.62319401 0.87051726
##  [7] 0.21836772 0.02032796 0.29164721 0.62715972

the result, e.g.

set_units(10, m/s)
## 10 [m/s]

literally means “10 times 1 m divided by 1 s”. In writing, the “1” values are omitted, and the multiplication is implicit.

Unit conversion

When conversion is meaningful, such as hours to seconds or meters to kilometers, conversion can be done explicitly by setting the units of a vector

b = a
units(b) <- make_units(km/h)
b
## Units: [km/h]
##  [1] 3.06633409 0.32615934 0.90226374 2.71503715 2.24349844 3.13386215
##  [7] 0.78612379 0.07318065 1.04992995 2.25777499

Basic manipulations

Arithmetic operations

Arithmetic operations verify units, and create new ones

a + a
## Units: [m/s]
##  [1] 1.70351894 0.18119963 0.50125763 1.50835397 1.24638802 1.74103453
##  [7] 0.43673544 0.04065592 0.58329441 1.25431944
a * a
## Units: [m^2/s^2]
##  [1] 0.7254941952 0.0082083266 0.0628148033 0.5687829279 0.3883707738
##  [6] 0.7578003063 0.0476844609 0.0004132259 0.0850580936 0.3933293136
a ^ 2
## Units: [m^2/s^2]
##  [1] 0.7254941952 0.0082083266 0.0628148033 0.5687829279 0.3883707738
##  [6] 0.7578003063 0.0476844609 0.0004132259 0.0850580936 0.3933293136
a ** -2
## Units: [s^2/m^2]
##  [1]    1.378371  121.827511   15.919814    1.758140    2.574859    1.319609
##  [7]   20.971192 2419.983800   11.756671    2.542399

and convert to the units of the first argument if necessary:

a + b # m/s + km/h -> m/s
## Units: [m/s]
##  [1] 1.70351894 0.18119963 0.50125763 1.50835397 1.24638802 1.74103453
##  [7] 0.43673544 0.04065592 0.58329441 1.25431944

Currently, powers are only supported for integer powers, so using a ** 2.5 would result in an error.

Unit simplification

There are some basic simplification of units:

t <- make_units(s)
a * t
## Units: [m]
##  [1] 0.85175947 0.09059982 0.25062882 0.75417699 0.62319401 0.87051726
##  [7] 0.21836772 0.02032796 0.29164721 0.62715972

which also work when units need to be converted before they can be simplified:

t <- make_units(min)
a * t
## Units: [m]
##  [1] 51.105568  5.435989 15.037729 45.250619 37.391641 52.231036 13.102063
##  [8]  1.219678 17.498832 37.629583

Simplification to unit-less values gives the “1” as unit:

m <- make_units(m)
a * t / m
## Units: [1]
##  [1] 51.105568  5.435989 15.037729 45.250619 37.391641 52.231036 13.102063
##  [8]  1.219678 17.498832 37.629583

Allowed operations that require convertible units are +, -, ==, !=, <, >, <=, >=. Operations that lead to new units are *, /, and the power operations ** and ^.

Mathematical functions

Mathematical operations allowed are: abs, sign, floor, ceiling, trunc, round, signif, log, cumsum, cummax, cummin.

signif(a ** 2 / 3, 3)
## Units: [m^2/s^2]
##  [1] 0.242000 0.002740 0.020900 0.190000 0.129000 0.253000 0.015900 0.000138
##  [9] 0.028400 0.131000
cumsum(a)
## Units: [m/s]
##  [1] 0.8517595 0.9423593 1.1929881 1.9471651 2.5703591 3.4408764 3.6592441
##  [8] 3.6795720 3.9712192 4.5983790
log(a) # base defaults to exp(1)
## Units: [(ln(re 1 m.s-1))]
##  [1] -0.1604511 -2.4013031 -1.3837823 -0.2821282 -0.4728974 -0.1386677
##  [7] -1.5215749 -3.8957581 -1.2322104 -0.4665540
log(a, base = 10)
## Units: [(lg(re 1 m.s-1))]
##  [1] -0.06968303 -1.04287269 -0.60096900 -0.12252672 -0.20537673 -0.06022261
##  [7] -0.66081156 -1.69190623 -0.53514218 -0.20262184
log(a, base = 2)
## Units: [(lb(re 1 m.s-1))]
##  [1] -0.2314820 -3.4643481 -1.9963758 -0.4070250 -0.6822467 -0.2000552
##  [7] -2.1951685 -5.6203908 -1.7777038 -0.6730952

Summary functions

Summary functions sum, min, max, and range are allowed:

sum(a)
## 4.598379 [m/s]
min(a)
## 0.02032796 [m/s]
max(a)
## 0.8705173 [m/s]
range(a)
## Units: [m/s]
## [1] 0.02032796 0.87051726
make_units(min(m/s, km/h)) # converts to first unit:
## 0.2777778 [m/s]

Printing

Following difftime, printing behaves differently for length-one vectors:

a
## Units: [m/s]
##  [1] 0.85175947 0.09059982 0.25062882 0.75417699 0.62319401 0.87051726
##  [7] 0.21836772 0.02032796 0.29164721 0.62715972
a[1]
## 0.8517595 [m/s]

Subsetting

The usual subsetting rules work:

a[2:5]
## Units: [m/s]
## [1] 0.09059982 0.25062882 0.75417699 0.62319401
a[-(1:9)]
## 0.6271597 [m/s]

Concatenation

c(a,a)
## Units: [m/s]
##  [1] 0.85175947 0.09059982 0.25062882 0.75417699 0.62319401 0.87051726
##  [7] 0.21836772 0.02032796 0.29164721 0.62715972 0.85175947 0.09059982
## [13] 0.25062882 0.75417699 0.62319401 0.87051726 0.21836772 0.02032796
## [19] 0.29164721 0.62715972

concatenation converts to the units of the first argument, if necessary:

c(a,b) # m/s, km/h -> m/s
## Units: [m/s]
##  [1] 0.85175947 0.09059982 0.25062882 0.75417699 0.62319401 0.87051726
##  [7] 0.21836772 0.02032796 0.29164721 0.62715972 0.85175947 0.09059982
## [13] 0.25062882 0.75417699 0.62319401 0.87051726 0.21836772 0.02032796
## [19] 0.29164721 0.62715972
c(b,a) # km/h, m/s -> km/h
## Units: [km/h]
##  [1] 3.06633409 0.32615934 0.90226374 2.71503715 2.24349844 3.13386215
##  [7] 0.78612379 0.07318065 1.04992995 2.25777499 3.06633409 0.32615934
## [13] 0.90226374 2.71503715 2.24349844 3.13386215 0.78612379 0.07318065
## [19] 1.04992995 2.25777499

Conversion to/from `difftime`

From difftime to units:

t1 = Sys.time() 
t2 = t1 + 3600 
d = t2 - t1
(du = as_units(d))
## 1 [h]

vice versa:

(dt = as_difftime(du))
## Time difference of 1 hours
class(dt)
## [1] "difftime"

units in `matrix` objects

set_units(matrix(1:4,2,2), m/s)
## Units: [m/s]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
set_units(matrix(1:4,2,2), m/s * m/s)
## Units: [m^2/s^2]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

but

set_units(matrix(1:4,2,2), m/s) %*% set_units(4:3, m/s)
##      [,1]
## [1,]   13
## [2,]   20

strips units.

units objects in `data.frame`s

units in data.frame objects are printed, but do not appear in summary:.

set.seed(131)
d <- data.frame(x = runif(4), 
                    y = set_units(runif(4), s), 
                    z = set_units(1:4, m/s))
d
##           x             y       z
## 1 0.2064370 0.8463468 [s] 1 [m/s]
## 2 0.1249422 0.5292048 [s] 2 [m/s]
## 3 0.2932732 0.5186254 [s] 3 [m/s]
## 4 0.3757797 0.2378545 [s] 4 [m/s]
summary(d)
##        x                y                z       
##  Min.   :0.1249   Min.   :0.2379   Min.   :1.00  
##  1st Qu.:0.1861   1st Qu.:0.4484   1st Qu.:1.75  
##  Median :0.2499   Median :0.5239   Median :2.50  
##  Mean   :0.2501   Mean   :0.5330   Mean   :2.50  
##  3rd Qu.:0.3139   3rd Qu.:0.6085   3rd Qu.:3.25  
##  Max.   :0.3758   Max.   :0.8463   Max.   :4.00
d$yz = with(d, y * z)
d
##           x             y       z            yz
## 1 0.2064370 0.8463468 [s] 1 [m/s] 0.8463468 [m]
## 2 0.1249422 0.5292048 [s] 2 [m/s] 1.0584095 [m]
## 3 0.2932732 0.5186254 [s] 3 [m/s] 1.5558761 [m]
## 4 0.3757797 0.2378545 [s] 4 [m/s] 0.9514180 [m]
d[1, "yz"]
## 0.8463468 [m]

Formatting

Units are often written in the form m2 s-1, for square meter per second. This can be defined as unit, and also parsed by as_units:

(x = 1:10 * as_units("m2 s-1"))
## Units: [m^2/s]
##  [1]  1  2  3  4  5  6  7  8  9 10

udunits understands such string, and can convert them

y = 1:10 * make_units(m^2/s)
x + y
## Units: [m^2/s]
##  [1]  2  4  6  8 10 12 14 16 18 20

Printing units in this form is done by

deparse_unit(x)
## [1] "m2 s-1"

Plotting

Base scatter plots and histograms support automatic unit placement in axis labels. In the following example we first convert to SI units. (Unit in needs a bit special treatment, because in is a reserved word in R.)

mar = par("mar") + c(0, .3, 0, 0)
displacement = mtcars$disp * as_units("in")^3
units(displacement) = make_units(cm^3)
weight = mtcars$wt * 1000 * make_units(lb)
units(weight) = make_units(kg)
par(mar = mar)
plot(weight, displacement)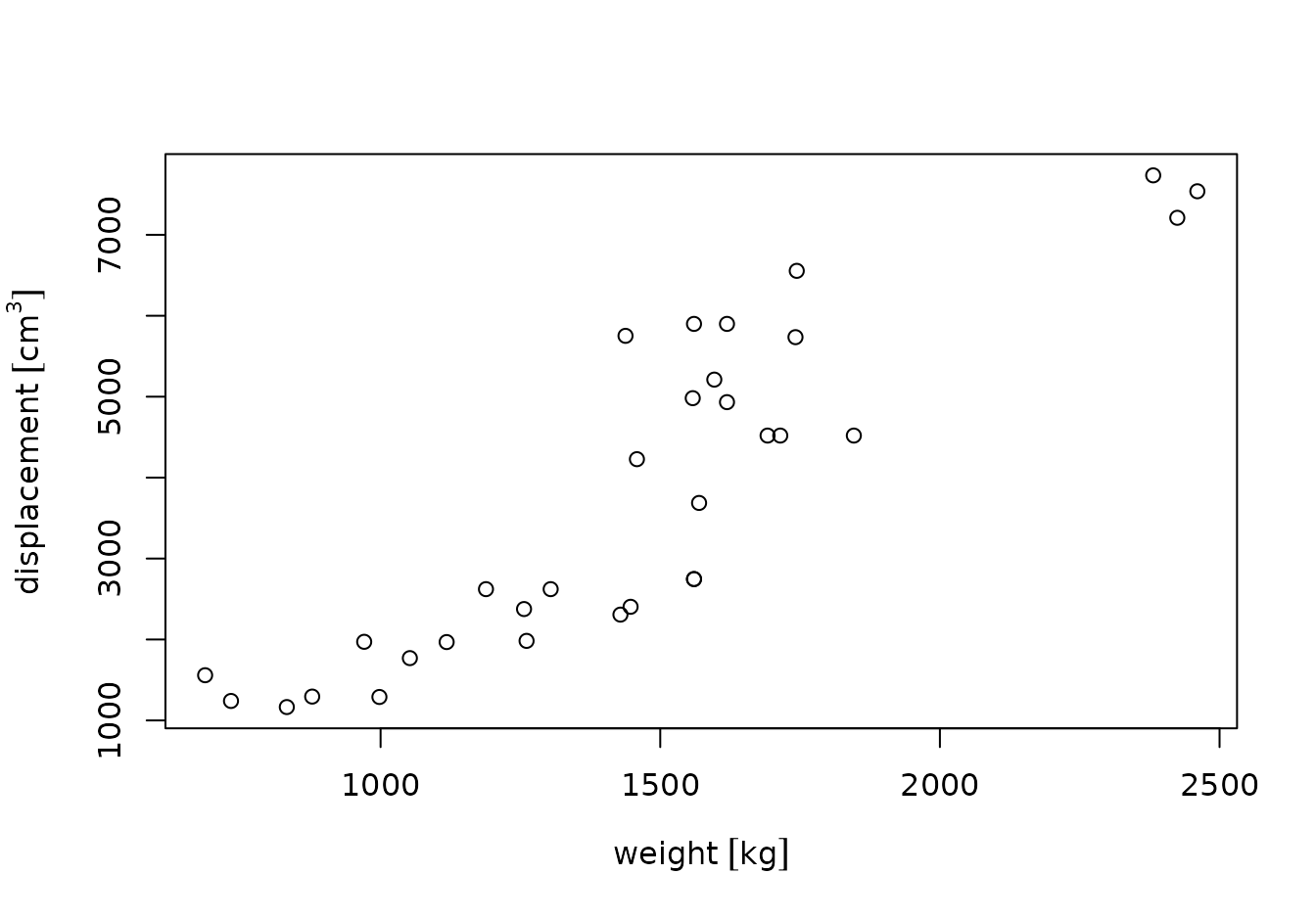

We can change grouping symbols from [ ] into ( ):

units_options(group = c("(", ")") )  # parenthesis instead of square brackets
par(mar = mar)
plot(weight, displacement)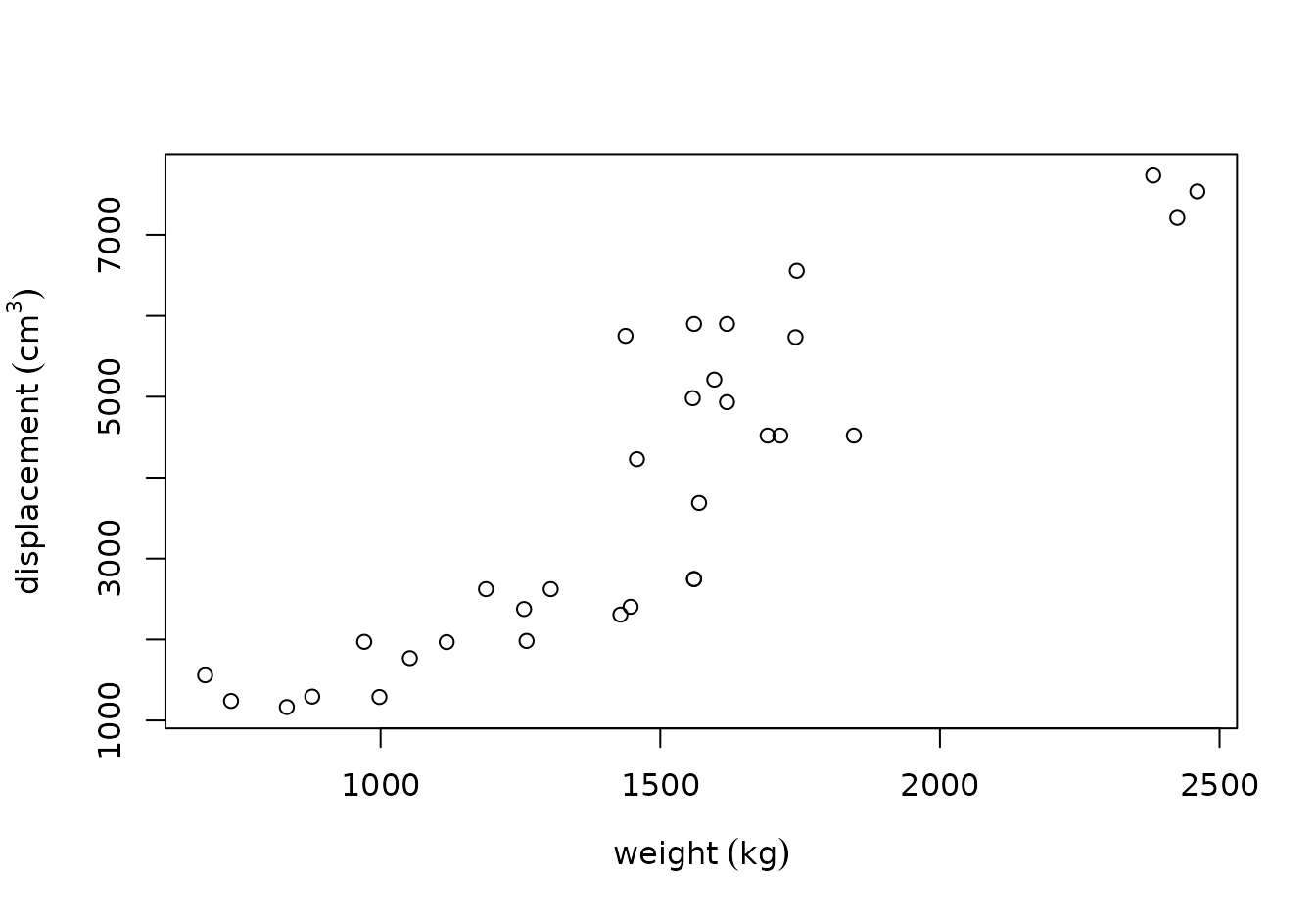

We can also remove grouping symbols, increase space between variable name and unit by:

units_options(sep = c("~~~", "~"), group = c("", ""))  # no brackets; extra space
par(mar = mar)
plot(weight, displacement)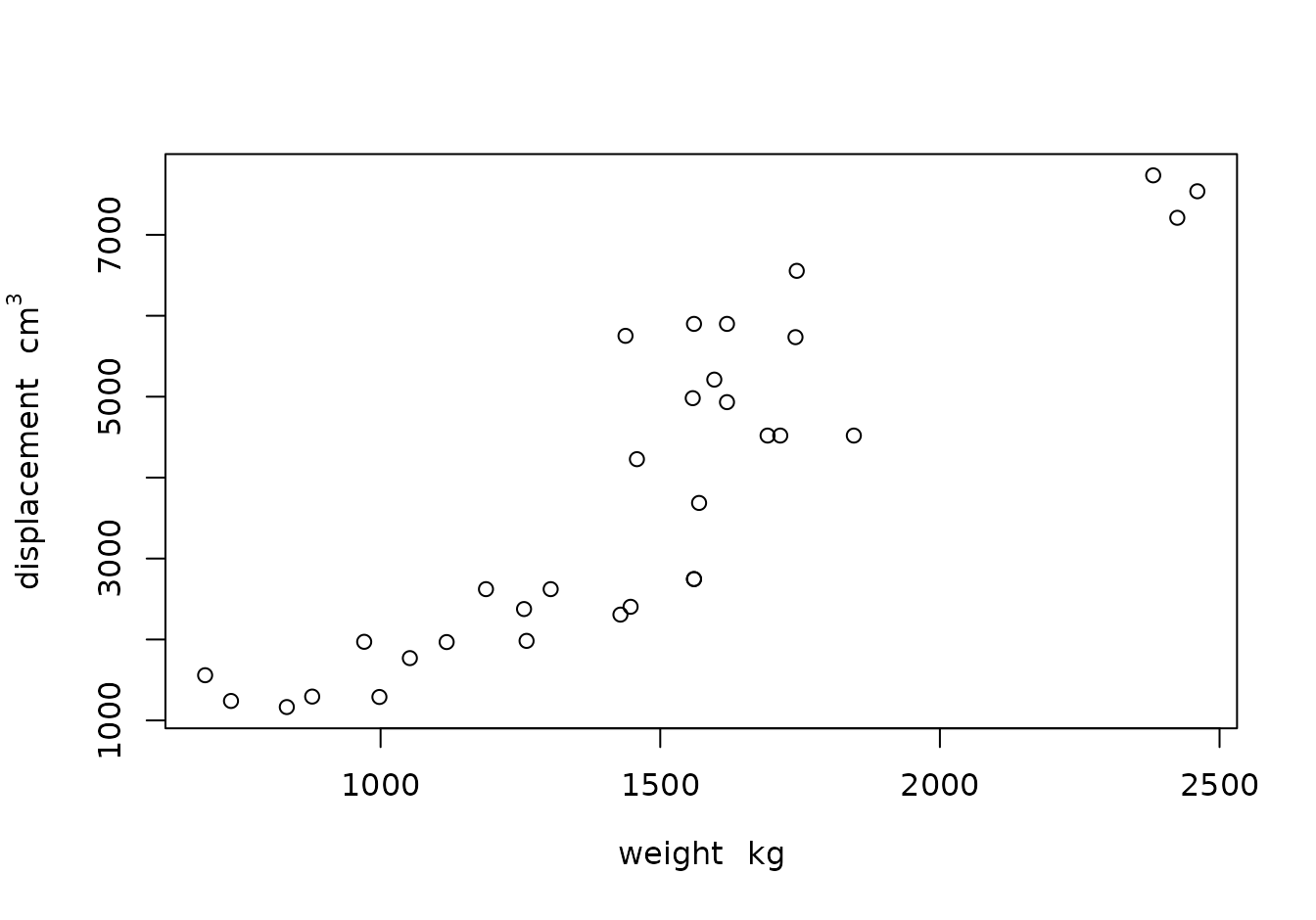

More complex units can be plotted either with negative powers, or as divisions, by modifying one of units’s global options using units_options:

gallon = as_units("gallon")
consumption = mtcars$mpg * make_units(mi/gallon)
units(consumption) = make_units(km/l)
par(mar = mar)
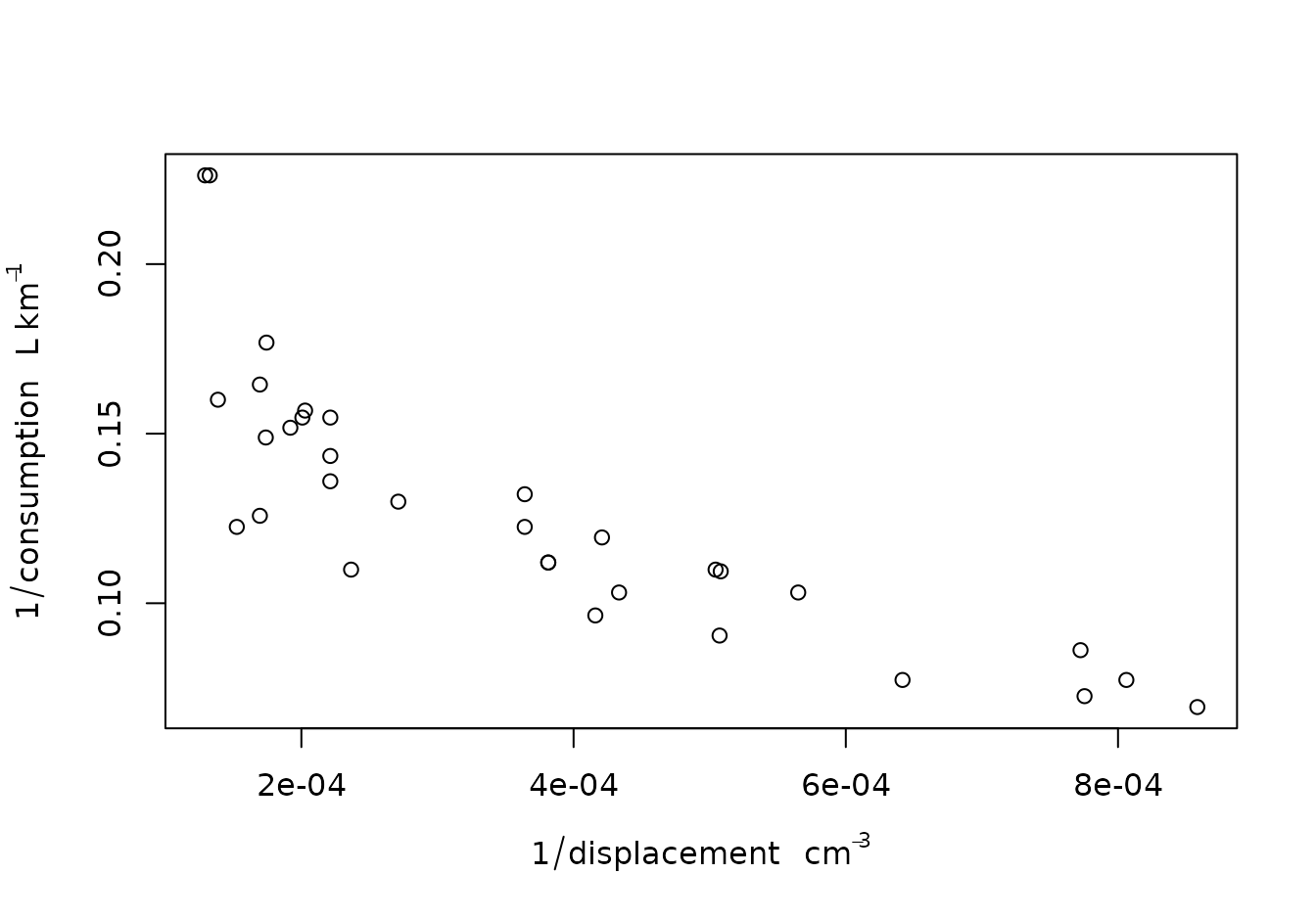
plot(displacement, consumption) # division in consumption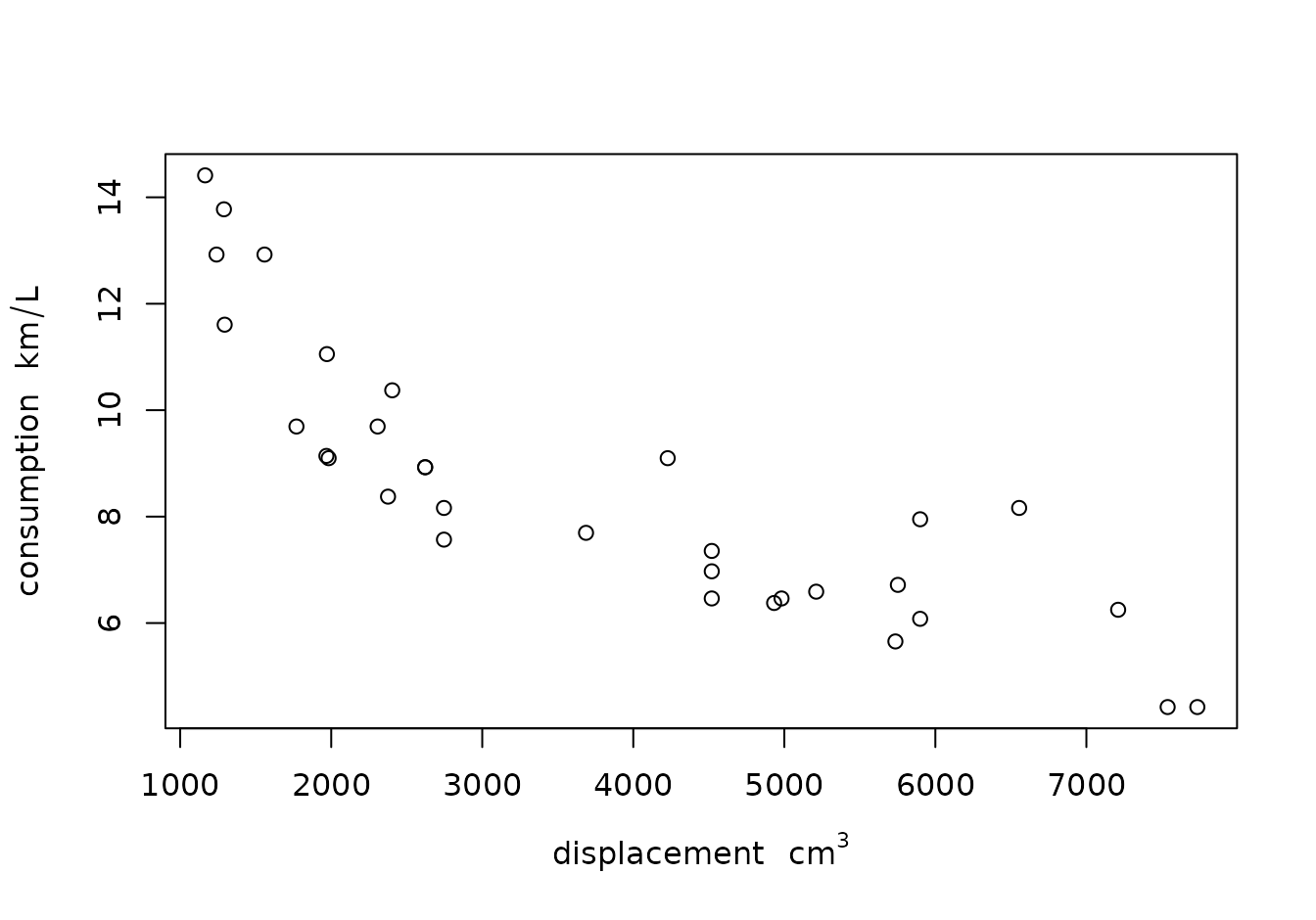

units_options(negative_power = TRUE) # division becomes ^-1
plot(displacement, consumption) # division in consumption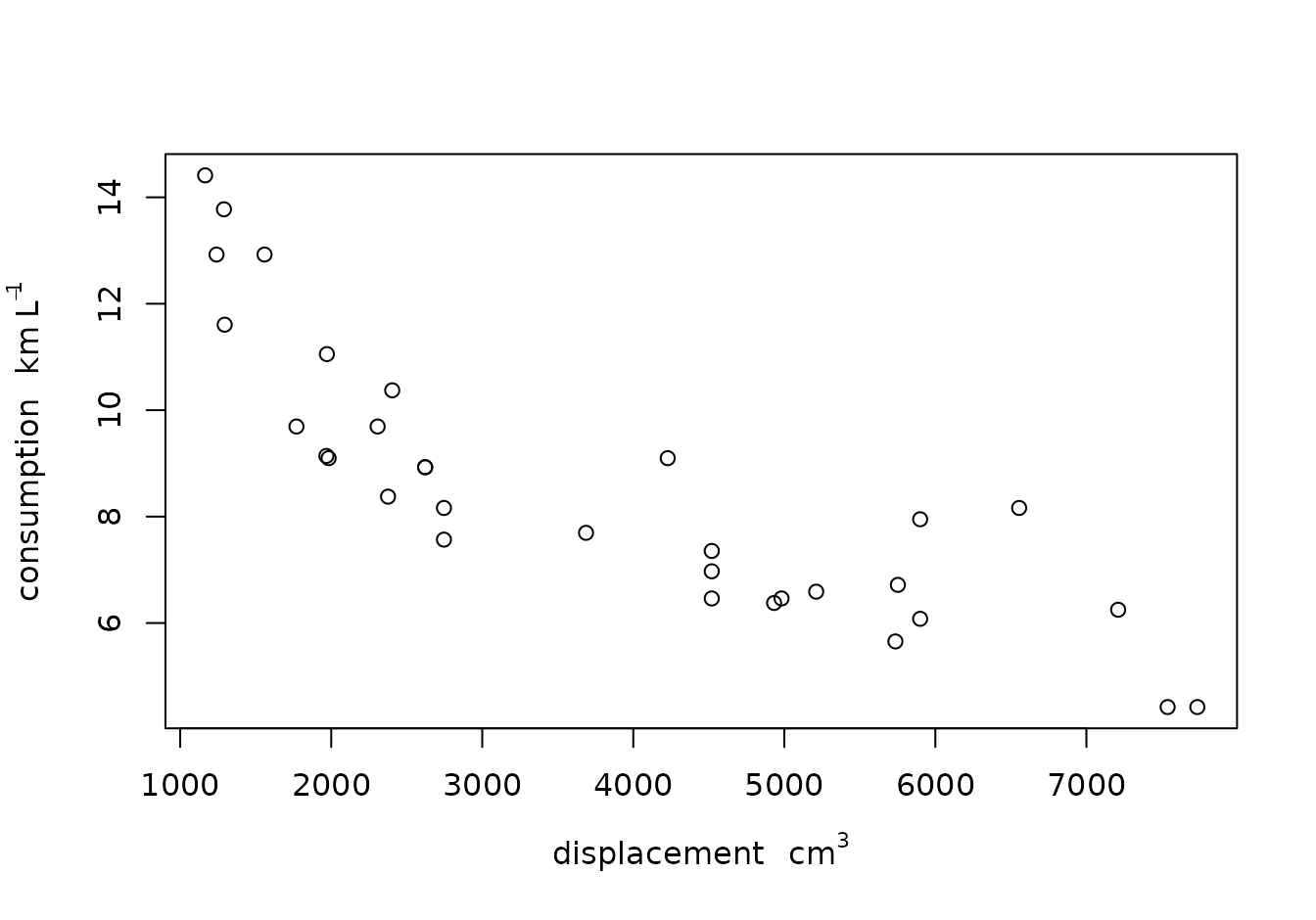

As usual, units modify automatically in expressions:

units_options(negative_power = TRUE) # division becomes ^-1
par(mar = mar)
plot(displacement, consumption)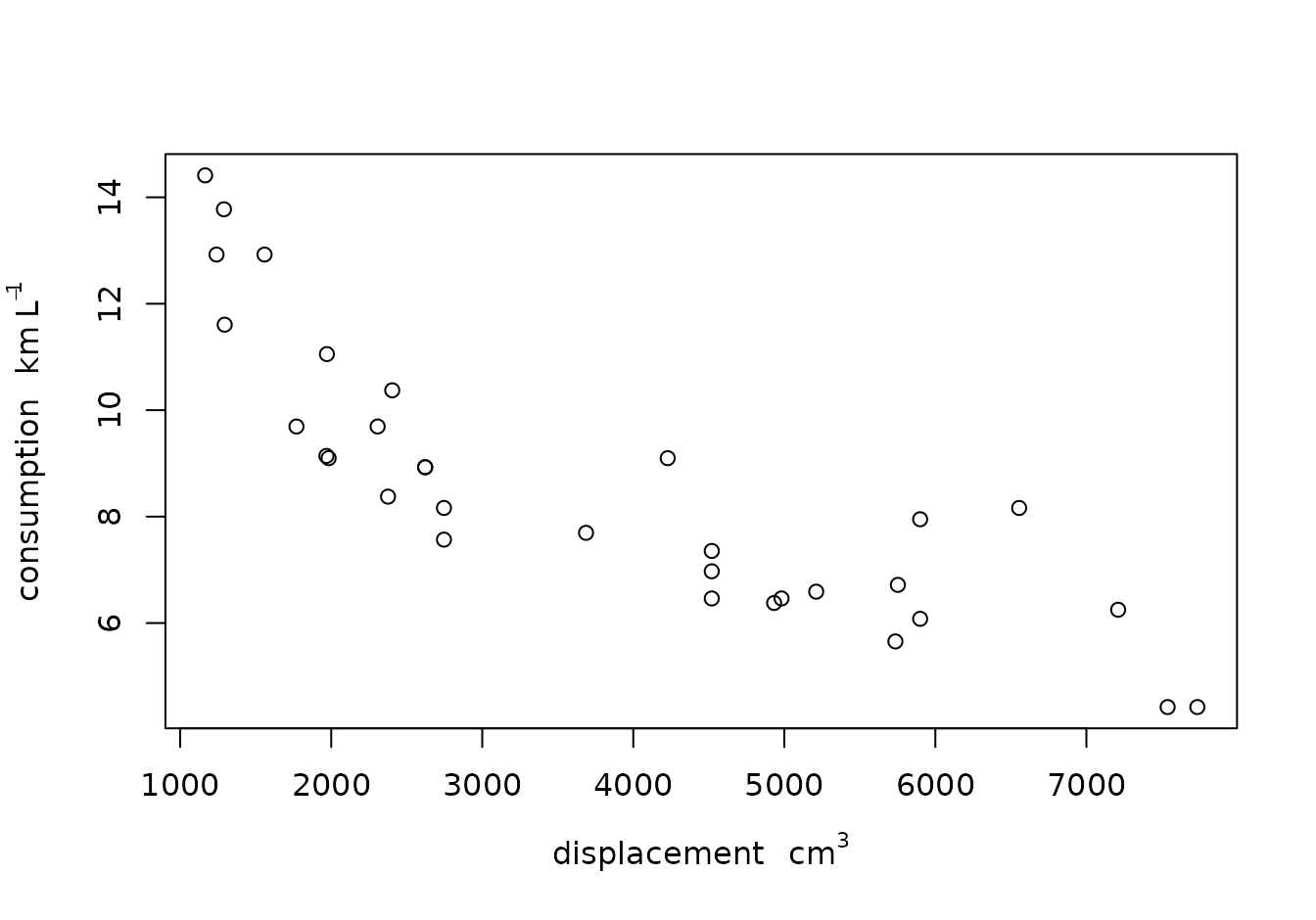

plot(1/displacement, 1/consumption)